ISSN: 0973-7510
E-ISSN: 2581-690X
The lack of adequate assessment methods for pathogens especially in food is a critical problem in microbiology. Traditional predictive methods are not able to accurately describe the trend of low-density bacterial growth behavior observed in the laboratory. The purpose of this study was to leverage state-of-the-art of machine learning algorithms (MLA) to develop a predictive model for bacterial growth of Proteus mirabilis after treatment of bay leaf extract. The experimental data are fitted to three models, namely logistic, Gompertz, and Richard models. These models are trained using simulation data and a curve-fitting optimization algorithm in MATLAB called fminsearch is applied to the data to obtain the optimal parameters of the models. The results show that this method provides a breakthrough in bacterial growth modeling. Various forms of mathematical models such as Gompertz, Richard, and others are no longer necessary to model bacterial behavior. Additionally, the generated model can help microbiologists in understanding the growth characteristics of bacteria after disinfectant treatment, and provides a theoretical reference and a method of risk management for better assessment of pathogens in food.
Algorithm, Machine Learning, Proteus mirabilis, Rotten Eggs, Specific Growth Rate
Proteus mirabilis is a species of pathogenic bacterium that causes various infections. This pathogen easily contaminates water bodies, soils, sewage, garden vegetables, and many others, and causes acute diarrhea, particularly acute enteritis among people under 10 years old. Other diseases, such as urinary tract infections and kidney stones may also be induced by P. mirabilis infection.1
Proteus mirabilis is a species belonging to the genus of Proteus with the capability to produce endotoxins that facilitate the induction of inflammatory responses and the formation of hemolysins. In humans, approximately 90% of Proteus infections are caused by Proteus mirabilis. Recent studies reported that this bacterial pathogen may trigger the formation of struvite stones following urinary tract infections, and is characterized by an increase in urine pH to alkaline.2 Its ability to produce urease enables this pathogen to hydrolyze urea and liberate ammonia (NH3) in the biochemical reaction catalyzed by such enzyme. 3
Recently, the assessment of microbiological food safety uses traditional microbial counting methods. Such methods have been evaluated as labor incentive, time-consuming, and have noncumulative research tools.4 Predictive mathematical models were developed to evaluate food-borne pathogens in food matrices under real-time conditions.5 The study of predictive microbiology combines mathematical modeling and the response of bacterial multiplication/inactivation to several factors, such as temperature, pH, and water activity.6
Predictive microbiology is a useful tool in the estimation of microbial behavior during food processing and storage.6 The primary model represents growth data under constant environmental conditions while the secondary model describes the growth data under constant environmental conditions.7 Primary models such as the Gompertz, Logistic, and Richard model and their modifications are often used to adjust microbial growth data.8,9 See also the more recent publications discussing the use of Gompertz model to analyze growth process.10,11 There are numerous sorts of auxiliary models utilize to estimate microbial development under dynamic conditions. These include the adjusted Richard model, response surface model, Ross cardinal model, and artificial neural networks.12 Therefore, the performance models used in the prediction depend on the overall accuracy of both primary and secondary models.
Before MLA was developed, microbiological modeling still used the traditional regression method, which was still based on empirical regression in microbiological modeling. This conventional deterministic model has been reported that it cannot precisely estimate the behavior of low cell density because it ignores single-cell variability (for example variation in cell generation time or individual inactivation time) that is thought to describe an inherent individual cell heterogeneity.13,14
In the last 2 decades, mathematical models with stochastic parameters have developed very rapidly.11,13-15 and widely applied in single-cell modeling which is indeed a stochastic parameter distribution.15 The growth of stochastic modeling has encouraged the application of machine learning modeling in predictive microbiology with varying performances to be developed. In many cases, machine learning models do not depend on extra recommendations or well recognized instruments to determine models and can learn predicted input and target features.16,17
The machine learning algorithm can learn more complex models through the data by training a large number of parameters, making it possible to produce precise forecast. 18-21 Additionally, deep neural network has already appeared excellent performance in modeling the growth limit of Bacillus spp. spores and growth rate of E. coli.22,23 However, no machine learning-based curve fitting has yet to be developed that can predict single-cell lag times of foodborne pathogens, which is important for future application of machine learning in microbiological risk evaluation.24-27
The objective of this study was to predict the maximum specific growth rate of the asymptote and the maximum value reached (µm), and the lag time (λ) of Proteus mirabilis. The Logistic model is fitted to the growth data of Proteus mirabilis and MLA were used to train and validate the model, so that it can accurately predict various unseen data of Proteus mirabilis.28
Methods for determining the growth kinetics of Proteus mirabilis
The growth kinetics of P. mirabilis was studied in a phosphate buffer medium supplemented with 10% v/v sterile albumen of duct egg, in a 1000 mL of Erlenmeyer flask with a working volume of 400 mL. This medium was then inoculated with 1 mL suspension of P. mirabilis previously incubated in nutrient broth medium for 24 hours at 30°C, placed on a shaker (with the speed of 100 rpm) at ambient temperature for 15 hours. Samples were collected periodically with an interval time of 1 hour and subjected to cell density determination by applying a serial dilution and spread method. Soon after inoculation (to), 1 mL of this inoculated medium was pipetted and added into 9 mL saline solution to obtain a dilution rate of 10-1. This bacterial suspension was further diluted to 10-5-10-7 (depend on suspension turbidity) by applying the same procedure. A volume of 0.1 mL of bacterial suspension from dilution rates of 10-3 – 10-4 or those from 10-5-10-7 was evenly spread on a sterile nutrient agar medium (in Petri dishes), incubated for 48 hours to 72 hours at 30°C, and counted for growing bacterial colonies. Petri dishes with 30 – 300 growing bacterial colonies only were counted, with the assumption that each colony originated from 1 cell. The study was terminated when the bacterial suspension reached the stationary phase of its growth. Five replications were prepared to obtain representative data, and the results were averaged.
Fitting of the growth models
In general, mathematical models that represent growth are presented in the form of a sigmoidal curve which generally contains parameters a, b, and c.10 These parameters have no meaning in biology. The difficulty that arises when mathematical models are written involving parameters without biological meaning is when determining initial values for parameter estimation. In addition, parameters such as a, b or c will make it difficult to determine the 95% confidence interval. Therefore, the mathematical model of growth was rewritten so that a mathematical model of biological parameters was obtained, namely: A, µm, and λ where A is the asymptote, µm is the maximum specific growth, and λ is the lag time. This model is known as a secondary model. The following discussion is about deriving the secondary logistic model. Consider the following primary logistic model as:
y(t) = a / 1 + exp (b – ct) … (1)
The inflection point of the curve is obtained by carrying out twice the differentiation of the function with respect to t This gives:
(dy(t))/dt = ac2 exp(b-ct) (1+exp(b-ct) )-2 …(2)
(d2 y(t))/(dt2 )=(ac2 exp(b-ct) (exp(b-ct)-1))/(1+exp(b-ct) )3 …(3)
The inflection point is reached when the second derivative is equal to zero or d2y / dt2 = 0. This gives t* = b/c. Subsequently, an expression µm is derived by taking the first derivative at the turning point (t* = b/c) or µm = ac/4 or c = 4 µm/a. The tangent passing through t* is given by:
y(t) = µm (t- t*) + a / 2 …(4)
The intersection between the tangent line and X axis is given by:
0 = µm (λ – t*) + a / 2 or λ = b – 2) /c or b = λc+2
The asymptotic value is reached t → for giving or y → a or A = a . Now, the substitution of all values a, b and c into (1), give:
y(t)= A/(1+exp((4μ_m)/A (λ-t)+2) ) …(5)
Similarly, for Gompertz model y(t) = a exp (- exp (b – ct)), gives the secondary (modified) Gompertz model of the form:
y(t)= A exp(-exp((μ_m e)/A (λ-t)+1) ) …(6)
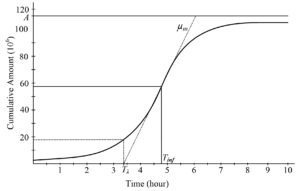
Bacterial growth frequently performs a phase where the µ starts at a zero value and then accelerates to a maximum value (µm) a while, causing a time lag (λ). After that, the growth curve reaches a stationary stage where the growth rate starts to decrease, and eventually reaches zero. At this point, the asymptote (A) is reached. When the growth curve is characterized as the logarithm of the number of organisms graphed with respect to time, this change produces an as-curve (Figure 1), with a l just after t = 0. This is followed by an exponential growth phase and then by an equilibrium stage.
Figure 1. Shape characteristics of sigmoidal growth curve describing bacteria dynamics: A upper asymptote; µm maximum absolute growth rate represented by the tangent at an inflection – slope at an inflection (dashed line); Tinf: time at an inflection; Tl : lag time
The nonlinear equations were fitted to P. mirabilis growth data by nonlinear regression with function fitnlm in MATLAB. This search method is used to find the minimum error produced by the differences between the estimated and experimental data. The function directly determines the initial values by searching for the steepest ascent of the curve. This is done by crossing the line through the x-axis and by taking the final point as an estimation of (A). The procedure then determines the growth of the parameter with the minimum error (5% significant error).
Construction of the data set and machine learning models
The fitting of the Logistics, Gompertz, and Richard models to the experimental data was carried out by MATLAB R2022 software,5 using a non-linear least squares method and the trust-region reflective Newton algorithm. The initial parameters were chosen and selected from the experimental data. By applying this procedure, the interval with 95% confidence is established. Using equation 7, the performance of the primary model is assessed.
The next step of the application of MLA is performed. The model will be trained using simulated data. The training data set comprising N observation of t, written t = (t1, t2, …, tN)T, along with corresponding observational data of y, represented as y = (y1, y2, …yN)T. The next step aims to train the model (with training data), that is, find the coefficients a, b, c that best fit the data using optimization algorithm fminserch. This algorithm minimizes the cost function, in this case, the error y and the predicted, ypred. After the coefficients are estimated, it is necessary to measure the error between the real value (output variable y) and the predicted value ypred. This means finding parameters a, b and c that minimize the sum of squared errors
SSE=∑Ni=1 (yi – a/(1+exp(b-cti))2 …(7)
where the times are ti and the responses are yi , i = 1, …, N. The sum of squared errors is the objective function and it is used to evaluate the performance of the model.
Fitting Data
The best fit curve has been found by choosing the minimum value of the sum square error (SSE). This learning curve searches and gives the most robust parameters of a,b, and c and it may be considered as another approach to parameter estimation. We found that this MLA has higher flexibility than the traditional methods because it does not require excessive equation formulation that shows the connection between responses of P. mirabilis and explanatory factors. 29
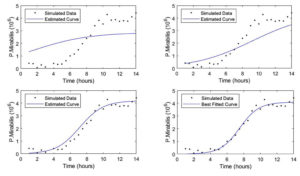
Figure 2. (a) Fitting of the Logistic growth models to the experimental data of the growth of Proteus mirabilis. (b) Simulated data used to train the growth model
As shown in Figure 2 (a), the plot of the experimental growth data of P. mirabilis comprising N = 14 data points is presented. The data is considered as the training dataset. The logistic model and the Gompertz are fitted to the data using30 (cftool) on Matlab 2021 giving best fit parameters for the Logistic model are a = 3.896 x 106, b = 7.646, c = 0.9472, for Gompertz are a= 4.01×10-6,b = 4.446, c= 0.6314, and for Richard model are a = 3.909 x 106, b = 0.8614, c = 0.8993, and d = 7.583. The traditional method stops after finding the fitted parameters. The models have not been trained with a new dataset. To train or test the curve with a new dataset, simulated data are used. The new data are generated by adding noises or errors to the experimental data.
In microbiology, the experimental data are difficult to collect because it is time-consuming and expensive. One approach to dealing with this is to generate data using simulations. The simulated data were produced by computation of the corresponding data and added with a small level of random noise characterized by normal distribution, y(t) = f(t;a, b, c) + rand(µ, s, n), µ and s are the mean and the standard deviation of the experimental data, see Figure 2b. The source of random noise could come from: a) sample of bacterial suspension is not 100% homogenous before spreading on the medium, b) viable cells in the samples (replicates) spread on the medium vary. Those lead to variations in cell numbers in the counting. Although an adjustable pipette was used in the sample transfer, the volume of the sample may vary at any time of sample transfer.
Figure 3. Convergence of the algorithm when applied to Logistic function with the initial value of a =4, b = 1, c = 1
The process of the learning curve is presented in Figure 3. The best fitted curve gives the minimum value of SSE 0.9678 with 126 iterations. Since parameters a,b, and c has no meaning in microbiology, the model has to be reparametrized in the form of a new model of growth known as a secondary model as given in equation (5) giving relationships:
a = A; b = 4µm / A λ + 2 ; c = 4µm / A
Substituting a = 3.896 x 106, b = 7.646, c = 0.9472, gives A = 3.896 x 106, µm = 0.9226, λ = 5.9605. We refer to Zwietering et al.,8 for the calculation of the secondary models of Gompertz and Ricard models. The calculation results are summarized in Table.
The value of a or A parameter for the three models is not significantly different. The availability of experimental data around A (asymptotic line) becomes an important issue due to its close relationship with other parameters, such as µm and l. Our result, µm and λ obtained for the logistic, Gompertz, and Richard models do not show a significant difference except for Richard models. This is due to the fact that Richard model involves 4 parameters. An additional experiment shows Gompertz models (3 parameters) and Richard (4 parameters) give the same prediction for µ(h) and λ (1/h) and µm and λ have a biologically similar meaning and the same units for all assessed models. However, our result shows that the doubling time for proteus mirabilis variates for the three models as seen in Table.
Table:
Summary results of parameter estimations.
| Parameters | Model | ||
|---|---|---|---|
| Logistic | Gompertz | Richard | |
| a | 3.896 x 106 | 4.010 x 106 | 3.939 x 106 |
| b | 7.646 | 4.446 | 0.8614 |
| c | 0.94722 | 0.6314 | 0.8993 |
| d | – | – | 7.583 |
| A | 3.896 x 106 | 4.010 x 106 | 3.909 x 106 |
| µm (h-1) | 9.226 x 105 | 9.314 x 105 | 9.180 x 105 |
| l (h) | 5.9607 | 5.4577 | 7.583 |
| v | – | – | 0.8614 |
| Doubling Time | 0.6449 | 0.3972 | 0.70422 |
Overall, it can be concluded, that further investigations are still needed to make the model perform well. Curve fitting machine learning algorithm has the potential as a new methodology for predicting µm and λ in Proteus mirabilis present in food. This algorithm is a breakthrough in bacterial growth modeling. With this algorithm, it no longer requires various forms of mathematical models such as Gompertz, Richard, and others.3 What is needed is a basic model, namely a sigmoid model with 3 or 4 parameters. The findings of our study are significantly important to help practitioners to comprehend growth characteristics of single-cell of P. mirabilis following disinfectant application and provide them with theoretical guidance for food companies and risk management for the improving assessments in foodborne-related pathogens.
ACKNOWLEDGMENTS
The authors would like to thank Integrated Lab for Biosciences and Biotechnology Udayana University for the provision of equipment during the research.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interest.
AUTHORS’ CONTRIBUTION
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
FUNDING
This study was funded by Institute of Research and Community Service, Udayana University under the letter of agreement No.: B/78450/UN14.4.A/PT.01.03/2021, April 21, 2021.
DATA AVAILABILITY
All datasets generated or analyzed during this study are included in the manuscript.
ETHICS STATEMENT
Not applicable.
- Esipov SE, Shapiro JA. Kinetic model of Proteus mirabilis swarm colony development. J Math Biol. 1998;36(3):249-268.
Crossref - Armbruster CE, Mobley HLT, Pearson MM. Pathogenesis of Proteus mirabilis Infection. EcoSal Plus. 2018;8(1).
Crossref - Zhao J, Gao J, Chen F, et al. Modeling and predicting the effect of temperature on the growth of Proteus mirabilis in chicken. J Microbiol Methods. 2014;99:38-43.
Crossref - McDonald K, Sun DW. Predictive food microbiology for the meat industry: a review. Int J Food Microbiol. 1999;52(1-2):1-27.
Crossref - Best A, Jubrail J, Boots M, Dockrell D, Marriott H. A mathematical model shows macrophages delay Staphylococcus aureus replication, but limitations in microbicidal capacity restrict bacterial clearance. J Theor Biol. 2020;497:110256.
Crossref - Fakruddin M, Mazumdar RM, Mannan KS bin. Predictive microbiology: Modeling microbial responses in food. Ceylon J Sci Biol Sci. 2011;40(2):121-131.
Crossref - Mahdinia E, Liu S, Demirci A, Puri VM. Microbial Growth Models. In: Demirci A, Feng H, Krishnamurthy K (eds). Food Safety Engineering. Springer, 2020.
Crossref - Zwietering MH, Jongenburger I, Rombouts FM, van ‘t Riet K. Modeling of the Bacterial Growth Curve. Appl Environ Microbiol. 1990;56(6):1875-1881.
Crossref - Muloiwa M, Nyende-Byakika S, Dinka M. Comparison of unstructured kinetic bacterial growth models. S Afr J Chem Eng. 2020;33:141-150.
Crossref - Tjorve KMC, Tjorve E. The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family. PLoS One. 2017;12(6):e0178691.
Crossref - Altilia S, Foschino R, Grassi S, Antoniani D, Dal Bello F, Vigentini I. Investigating the growth kinetics in sourdough microbial associations. Food Microbiol. 2021;99:103837.
Crossref - Esser DS, Leveau JHJ, Meyer KM. Modeling microbial growth and dynamics. Appl Microbiol Biotechnol. 2015;99(21):8831-8846.
Crossref - Koseki S, Koyama K, Abe H. Recent advances in predictive microbiology: theory and application of conversion from population dynamics to individual cell heterogeneity during inactivation process. Curr Opin Food Sci. 2021;39:60-67.
Crossref - Koutsoumanis KP, Lianou A. Stochasticity in Colonial Growth Dynamics of Individual Bacterial Cells. Appl Environ Microbiol. 2013;79(7):2294-2301.
Crossref - Baranyi J. Stochastic modelling of bacterial lag phase. Int J Food Microbiol. 2002;73(2-3):203-206.
Crossref - Munoz M, Guevara L, Palop A, Fernandez PS. Prediction of time to growth of Listeria monocytogenes using Monte Carlo simulation or regression analysis, influenced by sublethal heat and recovery conditions. Food Microbiol. 2010;27(4):468-475.
Crossref - Pin C, Baranyi J. Kinetics of Single Cells: Observation and Modeling of a Stochastic Process. Appl Environ Microbiol. 2006;72(3):2163-2169.
Crossref - Alonso AA, Molina I, Theodoropoulos C. Modeling Bacterial Population Growth from Stochastic Single-Cell Dynamics. Appl Environ Microbiol. 2014;80(17):5241-5253.
Crossref - Koutsoumanis KP, Lianou A, Gougouli M. Latest developments in foodborne pathogens modeling. Curr Opin Food Sci. 2016;8:89-98.
Crossref - Bemani A, Kazemi A, Ahmadi M. An insight into the microorganism growth prediction by means of machine learning approaches. J Pet Sci Eng. 2023;220:111162.
Crossref - Dieguez-Santana K, Gonzalez-Diaz H. Machine learning in antibacterial discovery and development: A bibliometric and network analysis of research hotspots and trends. Comput Biol Med. 2023;155:106638.
Crossref - Golden CE, Rothrock MJ, Mishra A. Comparison between random forest and gradient boosting machine methods for predicting Listeria spp. prevalence in the environment of pastured poultry farms. Food Res Int. 2019;122:47-55.
Crossref - Patra P, Disha BR, Kundu P, Das M, Ghosh A. Recent advances in machine learning applications in metabolic engineering. Biotechnol Adv. 2023;62:108069.
Crossref - Chitra M, Sutha S, Pappa N. Application of deep neural techniques in predictive modelling for the estimation of Escherichia coli growth rate. J Appl Microbiol. 2021;130(5):1645-1655.
Crossref - Puerta-Gomez AF, Moreira RG, Kim J, Castell-Perez E. Modeling the growth rates of Escherichia coli spp. and Salmonella Typhimurium LT2 in baby spinach leaves under slow cooling. Food Control. 2013;29(1):11-17.
Crossref - Huang L. Simulation and evaluation of different statistical functions for describing lag time distributions of a bacterial growth curve. Microb Risk Anal. 2016;1:47-55.
Crossref - Akkermans S, van Impe JFM. An Accurate Method for Studying Individual Microbial Lag: Experiments and Computations. Front Microbiol. 2021;12.
Crossref - Sarmah N, Mehtab V, Bugata LSP, et al. Machine learning aided experimental approach for evaluating the growth kinetics of Candida antarctica for lipase production. Bioresour Technol. 2022;352:127087.
Crossref - Koyama K, Kubo K, Hiura S, Koseki S. Is skipping the definition of primary and secondary models possible? Prediction of Escherichia coli O157 growth by machine learning. J Microbiol Methods. 2022;192:106366.
Crossref - King AP, Aljabar P. Machine learning. In: Matlab® Programming for Biomedical Engineers and Scientists. Elsevier. 2023:343-372.
Crossref
© The Author(s) 2023. Open Access. This article is distributed under the terms of the Creative Commons Attribution 4.0 International License which permits unrestricted use, sharing, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.